active and passive elliptic crossover
Sometimes you come across a driver which being good in all other respects has a sudden peak or trough in its response. If a peak then you might need a filter with a steep response to get the peak 20db down at least. Such a filter is the elliptic. Jason Cuadra did some work on it. Common filters are all pole networks. Elliptic fiters have zeros. Zeros give the notch neccesary for a steep slope. The location of the poles and zeros creates ripple behaviour in the passband, similar to a Chebychev filter. Sharp roll off is obtained at the expense of return lobes in the stop band. Cuadra’s article here:
silo.tips_jason-cuadras-elliptic-filters
Both Cuadra (passive) and Thiele (active) have achieved a good compromise of passband flatness, fairly steep rolloff and low stop band lobes while giving an economical design. More here for those of a mathematical bent:
https://www.analog.com/en/technical-articles/analog-filter-design-demystified.html
An extremely competent Japanese passive filter here:
http://www.gem.hi-ho.ne.jp/katsu-san/audio/Speaker/filters/index_en.html
And just cos I like it, Kyu Sakamoto with Sukiyaki:
https://www.youtube.com/watch?v=ETX_EJgOVw8
Kenny Ball captures the mood in this trad jazz version
https://www.youtube.com/watch?v=WeCAQmxq_Ew
I got a feel for the circuitry involved with an active approach both from Jasons work and Bob Ellis post here:
http://www.htguide.com/forum/showthread.php?18740-Active-Cauer-Elliptic-filter-design-in-20-minutes
Interesting discussion on Diyaudio about this type of filter:
http://www.diyaudio.com/forums/multi-way/6655-best-active-crossover-here.html
One way of achieving the notch is to use a bridged T network
http://johnhearfield.com/RC/RC4.htm
Analysis of the transposed RC version (note in this pdf Fig 3c is the equivalent of Fig 1c)
http://tf.nist.gov/general/pdf/2526.pdf
These 2 circuits surprisingly give the same response. Mathematical proof of this courtesy my friend JAG.
A great thing about the bridged-T is that the notch depth and frequency can be independently variable, a fact which seemed to be lost on the TI notch filter app writers who do not mention it. It is used on the classic Heathkit IG18 signal generator. Unfortunately when you improve the Q by using positive feedback around an op-amp the feedback resistor (R3 and R12 in the crossover circuit) changes the frequency as well as the Q. This may explain why the TI people do not like it, but if its good enough for Thiele, its good enough for me. I am being unfair to TI, having just found this interesting article on active filters
activefilt
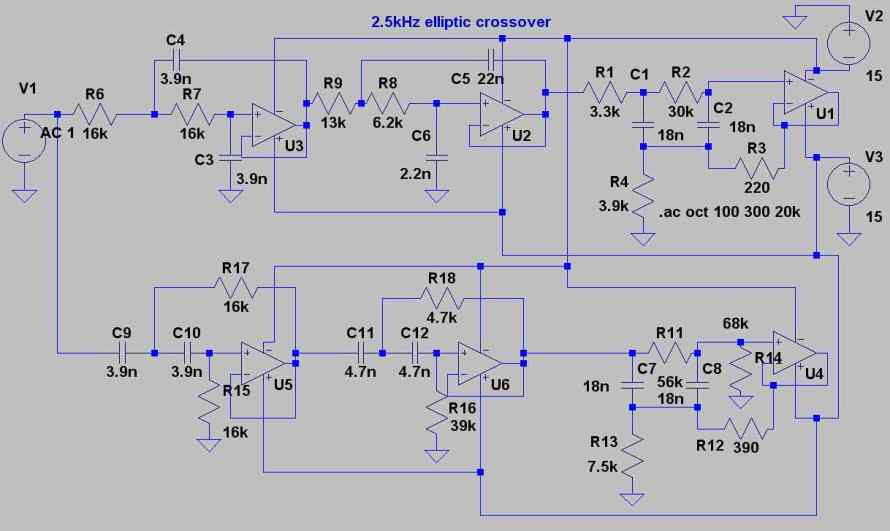
I consulted Thieles patent on it and came up with this circuit for a 2.5Khz crossover using components you might actually be able to buy. No doubt if I had used the exact values the curves would be symmetrical. Actually the two halves are virtually symmetrical . Its just that the Sallen/Key bit is centred on 2.555kHz and the Bridged T bit is centred on 2.6kHz. Since I was modifying an existing board, I wanted a single op-amp for the zero or notch circuit. Alternatives are a gyrator or the Jess & Schussler circuit. I found gyrator circuits inconsistent, change the op-amp and you get different results! Thieles patent has lapsed by the way.
This shows the modelled response. I tried this in practice using NE5532. It works fine, electronically. Connected up the speakers and found it works acoustically too. However you need drive units with a reasonably flat response. If the lack of symmetry bothers you, make R2 a 31.8k resistor by putting a 1.8k in series with the 30k and make R11 a 58.2k resistor by putting a 2.2k in series with the 56k. Following my tracking idea I modelled going up one value in the E12 series, i.e 4.7n instead of 3.9n etc. for each of the capacitors which gave me a crossover of 2.1kHz at -6.08dB . If you go down one value i.e 3.3nF instead of 3.9n etc you get a crossover of 3.1kHz at -5.9dB. The E24 resistor series is more sensitive than the E12 capacitor series so going up one value for each of the resistors gives 2.7kHz and down one gives 2.27kHz You need 0.1uF decoupling capacitors to ground on the op-amp supplies. You could use 2% PPS Panasonic 1210 chip capacitors with wires soldered on for the capacitors. 1% resistors are readily available. The ultimate slope is 24 db/octave of the 4th order sallen and key but near the crossover a higher slope kicks in. This approach does just enough to get a good response without going overboard on notch depth or whatever. A 257Hz crossover using the above circuit is here:
A thread recently came up on his subject on the Parts express forum and Jason Cuadra returned and joined in. Since I think his work was contemporary with Thieles there is the question of prior art. No taking away from Thiele his mastery of filters. The man is, of course a genius. My response shows the phase peaks and troughs which were discussed as a group delay issue. I personally think they occupy so little of the spectrum that they will not be noticed but no doubt the cynics will pooh-pooh this! Here is the thread:
http://techtalk.parts-express.com/showthread.php?t=219054
Here is a passive circuit using Cuadra’s scheme. It only needs one more capacitor than a fourth order crossover and gives much sharper slopes. The crossover is at 2.45kHz
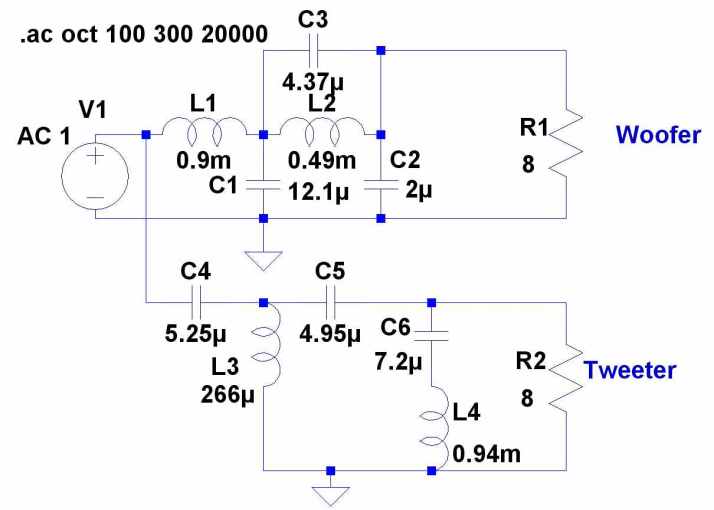
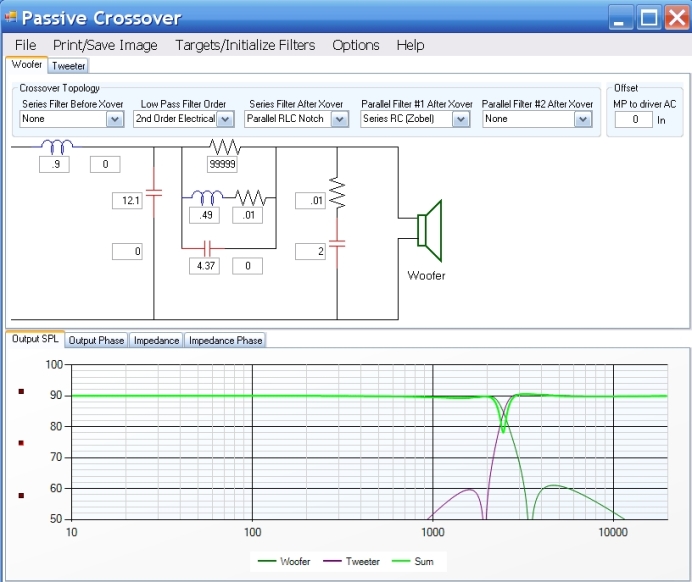
And here is the response. I found I needed a 10 ohm and 30uF zobel (not shown) on the woofer but no zobel on the tweeter. Also I did not initially get the modelled response on the tweeter. This was due to the 2 inductors in the circuit being too close together and giving mutual coupling which affected the response badly. I used the crossover on an unholy alliance of the Mission CP168 and the Monitor Audio metal dome tweeter mentioned in a later post. With the 25kHz resonance trap across the tweeter as well, it gave excellent results. Project name M&Ms For some reason I prefer the sound of the passive to the active verson which is unusual for me despite the bigger phase glitches.

Here it is modelled in Neil Davis’s PSD-lite which shows the tweeter has to be reverse wired:
🆕The HiVi M6N is on offer at Parts Express. It is a good candidate for the above crossover.
I have come across an alternative interesting technique to deal with a driver with sudden breakup:
http://www.diyaudio.com/forums/multi-way/277691-s-harsch-xo.html
The above link is an asymetric crossover I found a curious asymetric crossover going the other way in the 1980 National semi Audio handbook mentioned on Diyaudio
The elliptic circuits here were modelled in LTspice. Did you know that Spice is 40 years old?
http://edn.com/electronics-blogs/other/4311273/SPICE-a-40-year-old-open-source-success-story
Very useful tutorial on LTspice:
http://www.simonbramble.co.uk/lt_spice/ltspice_lt_spice.htm
Another useful tutorial on LTspice, courtesy Gunthard Kraus:
spice-simulation_using_ltspice_part_1
Part 2. How to design RF circuits using Ltspice
Segue into a Mathcad and LTspice analysis of a bass reflex speaker (in French)
https://2adiy.ovh/simul-hp.html
You can analyse your speaker with spice here:
http://users.on.net/~isaacmcn/audio/spice/spice.htm
More analysis here:
http://andyc.diy-audio-engineering.org/
Found a video of Thiele explaining his early work here:
http://www.youtube.com/watch?v=T3BbyYBrCJ8
He built on the previous work of Locanthi and Novak and created a scientific way of designing loudspeakers. His memorial is the parameters that bear his name. Unfortunately he published his work in an obscure journal so not many people knew about it. He also worked with Richard Small and Ernie Benson the “Sydney speaker mafia”
In honour of the Australian contribution to speaker design Jimmy Rodgers singing Waltzing Matilda:



Leave a comment